I 17 gruppi cristallografici

Fra tutti i modi diversi di decorare una superficie, qui ci occuperemo solo di quelli periodici, e cioè di quelli che hanno una struttura ripetitiva potenzialmente infinita, in cui un certo modulo viene utilizzato ripetutamente secondo un certo insieme di trasformazioni isometriche: traslazioni (almeno 2 diverse) rotazioni, riflessioni e glisso-simmetrie.
Anche con queste limitazioni i possibili pattern ripetitivi differenti sono in numero potenzialmente infinito. Tuttavia i matematici hanno dimostrato che esistono solo 17 modi diversi di assemblare le trasformazioni isometriche per ottenere uno schema periodico. Questi 17 diversi insiemi di trasformazioni perndono il nome di gruppi cristallografici (perchè sono di particolare utilità in cristallografia, la scienza che classifica i cristalli).
I vari gruppi possono essere identificati in modo molto semplice seguendo questo diagramma di flusso:



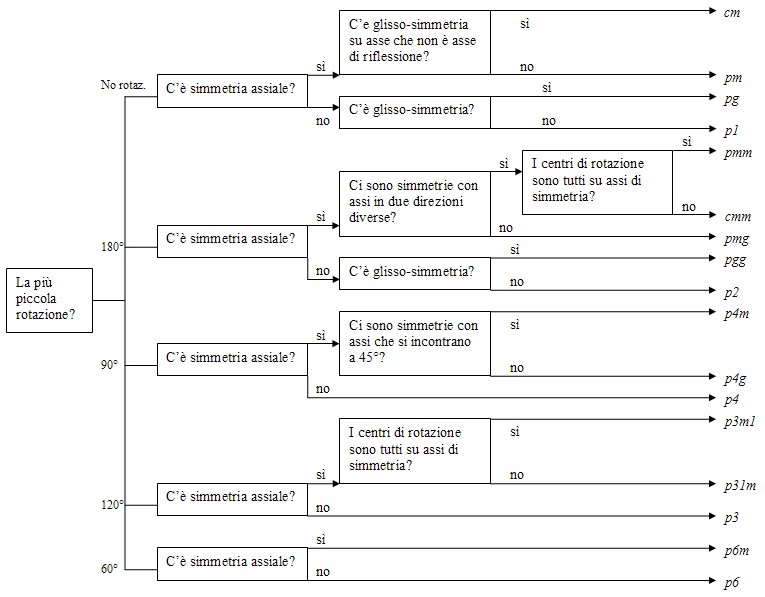Per classificare un disegno piano periodico basta rispondere alle varie domande che si succedono da sinistra a destra, e si ottiene così una delle 17 sigle che indicano i vari gruppi cristallografici.

Fra i diversi tipi di disegno ripetitivo sono particolarmente suggestive le cosiddette tassellazioni, cioè quei disegni periodici basati su uno o più (preferibilmente pochi) motivi differenti, chiamati tasselli, che si adattano l'un l'altro in modo da coprire tutto il piano senza sovrapposizioni e senza lasciare spazi vuoti fra l'uno e l'altro, come fanno le varie piastrelle di una pavimentazione.

Fra i maggiori artisti di questa specialità c'è Mauritius Cornelius Escher che ha elevato questa forma espressiva ai più alti livelli.
In queste pagine verranno analizzati alcuni dei suoi disegni periodici, tutti basati su un unico tassello.